1. Definitions
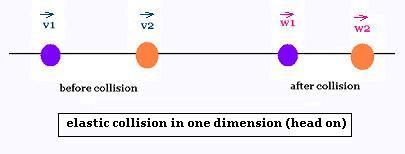
A collision is an interaction between two or more objects that occur in limited time and space. During a collision, the forces between the objects may be complicated. We examine just what goes into a collision and what comes out of the collision. We assume that the net external forces to the system of the interacting objects are negligible. Therefore, they will produce negiligible impulses, and thus the momentum of the system is conseved. That is The total momentum of the system before the collision is equal to the momentum of the system after the collision.
The main task, when studying collision is to determine the outgoing velocities regarding the incoming velocities. Just for a collision in one dimension, conservation of momentum gives one equation for the two unknown ougoing velocity components. The problem is in general unsolvable. The consrvation of energy can help.
The conservation of the kinetic energy is uesd only when the collision is callled elastic. Eelastic means no energy is lost in the collision. The collision in which the kinetic energy is not conserved are called inelastic collisions. In a macroscopic level, the collisions are often inelastic and the loss of energy is transformed into heat. In this level, collisions between steel balls at low speeds are taken as elstic. The collision are often elastic in the case of atomic interactions.
2. Elastic collisions : One dimension along the x-axis
Two objects of mass m1 and m2 and initial velocoties v1 and v2 collide and take the velocities w1 and w2. The conservation of the momentum is written as:
m1v1 + m2v2 = m1w1 + m2w2 (2.1)
The conservation of the kinetic energy gives:
(1/2)m1v12 + (1/2)m2v22 = (1/2)m1w12 + (1/2)m2w22 (2.2)
Rewriting the equations (2.1) and (2.2), we find:
m1(v1 – w1) = – m2(v2 – w2)
m1(v12 – w12) = – m2(v22 – w22)
Dividing (2.1) by (2.2) gives:
1/(v1 + w1) = 1/(v2 + w2) or (v1 + w1) = (v2 + w2) or
Elastic collision:
v1 – v2 = – (w1 – w2) (2.3)
In an elastic collision, the relative velocity is just reversed.
3. Elastic collisions: different cases
3.1. v2 = 0: the second object is stationary
If the object m2 is at rest, that is v2 = 0, then for the equations (2.1) and (2.2):
m1v1 = m1w1 + m2w2
m1v12 = m1w12 + m2w22
Or Putting (2.3) in (2.1) with v2 = 0 gives:
v1 = – (w1 – w2) gives w2 = v1 + w1, so
m1v1 = m1w1 + m2(v1 + w1), that gives:
w1 = v1 (m1 – m2)/(m1 + m2), and
w2 = v1 + w1 = [(m1 + m2)v1 + v1(m1 – m2) ]/(m1 + m2) = 2m1 v1/(m1 + m2)
v2 = 0:
w1 = v1 (m1 – m2)/(m1 + m2), and
w2 = 2m1 v1/(m1 + m2)
3.2. equal masses m1 = m2 = m
3.2.1 case v2 = 0
In this case we have:
w1 = v1 (m1 – m2)/(m1 + m2) = 0
w2 = 2m1 v1/(m1 + m2) = v1
The two objects exchange the velocities.
3.2.2: case v2 not null
In this case we have:
v1 + v2 = w1 + w2
v1 – v2 = -(w1 – w2)
Adding and subtracting gives: v1 = w2 , and
v2 = w1
The two objects exchange the velocities in this head on collision.
3.3. v2 = 0 and m1>> m2
From the results of 3.1., we have:
w1 = v1 (m1 – m2)/(m1 + m2) ? v1
w2 = 2m1 v1/(m1 + m2) ? 2v1
The incoming object 1, with large mass, keeps pratically its initial velocity, while the small object 2, initially at rest, moves off at twice the velocity of the projectile object 1
3.4. v2 = 0 and m1<< m2
From the results of 3.1., we have:
w1 = v1 (m1 – m2)/(m1 + m2) ? – v1
w2 = 2m1 v1/(m1 + m2) ? 2(m1/m2) v1 ? 0
The incoming object 1, with small mass, bounces back with the same speed that it had, while the large object 2, initially at rest, remains undisturbed.
3.5. General case
The reltaed algebra to determine the final speeds w1 and w2 is straightforward, but tedious. Using The center of mass, we have found:
w1 = (m1 – m2)v1/M + 2m2v2/M
w2 = (m2 – m1)v2/M + 2m1v1/M
4. Inelastic collisions
4.1. Definitions
A collision is inelastic when there is a loss of energy during the collision. Hence the kinetic energy of the related system is npt conserved. But the momentum is always conserved. The inelastic collision in which the projectile and the target stick together is called completely inelastic.
For a completely inelastic collision (m1,v1) + (m2,v2), the coonservation of the momentum gives directly the searched value w of the system, w = (m1 v1 + m2 V2)/(m1 + m2) = speed of the center of mass.
4.2. Example: Rocket motion
From an inertial frame at rest: vr is the velocity of the rocket, and vg is the velocity of the exhaust gazes. vgr is the velocity of the exhaust gases in the rocket frame. We have as vectors :
vg = vr + vgr
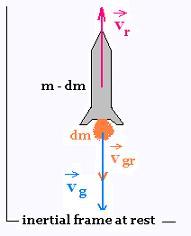
At first, the system (rocket + gases) has an initial momentum Pi = m vr a fixed time t. At a later time, the momentum of the system is: Pf = (m – ?m)(vr + ?vr) + (? m)vg. The problem is considered in one dimention, then:
vg = vr – vgr (1)
Pi = m vr (2)
Pf = (m – ?m)(vr + ?vr) + (? m)vg (3)
? m is negative
? P = Pf – Pi = (m – ?m)(vr + ?vr) + (? m)vg – m vr =
– ?m vr + m ?vr + ?m vg
Where the infinitesimal term ?vr?m is neglected. Therefore, according to the second Newton’s law:
? Fext = dP/dt = – (dm/dt) vr + m dvr/dt + (dm/dt) vg
Using the equation (1), we get:
? Fext = – (dm/dt) vr + m dvr/dt + (dm/dt) (vr – vgr) = + m dvr/dt – (dm/dt) vgr
or:
? Fext + (dm/dt) vgr = m dvr/dt
The term (dm/dt) vgr is the thrust force of the rocket.
m dvr/dt = ?Fext + vgr (dm/dt)
If ? Fext = 0, then: m dvr/dt = vgr (dm/dt), or
dvr = vgr (dm/m), dm is negative, hence:
Integrating from a speed v1r to v2rwith respect to the rocket, gives:
v2r – v1r = – vgr [Ln(m2) – Ln(m1)] = – vgr Ln(m2/m1)
If the chemical fuel of the rocket provides a speed of 3 km/s, what is the speed of the rocket when 7/10 of the fuel is burned ?
The initial speed v1r is set to zero. Therefore:
v2r = – vgr Ln(m2/m)
m2 = (10/10 – 7/10)m = (3/10)m
v2r = – 3 Ln(3/10) = 3.60 m/s.
Remark that the speed didn’t become much larger as we need. Building rockets in stages gives a solution. In this case, the final speed for a stage becomes the initial speed of the next following stage.
https://scientificsentence.net/Equations/Mechanics/collisions/index.php?key=yes&Integer=collisions